Introduction
本文为斯坦福大学CS231n课程作业及总结,若有错误,欢迎指正。
所有代码均已上传到GitHub项目cs231n-assignment2
Code
1. batch normalization forward
实现思路: 参考论文[1],通过如下公式计算
def batchnorm_forward(x, gamma, beta, bn_param):
"""
Forward pass for batch normalization.
During training the sample mean and (uncorrected) sample variance are
computed from minibatch statistics and used to normalize the incoming data.
During training we also keep an exponentially decaying running mean of the
mean and variance of each feature, and these averages are used to normalize
data at test-time.
At each timestep we update the running averages for mean and variance using
an exponential decay based on the momentum parameter:
running_mean = momentum * running_mean + (1 - momentum) * sample_mean
running_var = momentum * running_var + (1 - momentum) * sample_var
Note that the batch normalization paper suggests a different test-time
behavior: they compute sample mean and variance for each feature using a
large number of training images rather than using a running average. For
this implementation we have chosen to use running averages instead since
they do not require an additional estimation step; the torch7
implementation of batch normalization also uses running averages.
Input:
- x: Data of shape (N, D)
- gamma: Scale parameter of shape (D,)
- beta: Shift paremeter of shape (D,)
- bn_param: Dictionary with the following keys:
- mode: 'train' or 'test'; required
- eps: Constant for numeric stability
- momentum: Constant for running mean / variance.
- running_mean: Array of shape (D,) giving running mean of features
- running_var Array of shape (D,) giving running variance of features
Returns a tuple of:
- out: of shape (N, D)
- cache: A tuple of values needed in the backward pass
"""
mode = bn_param['mode']
eps = bn_param.get('eps', 1e-5)
momentum = bn_param.get('momentum', 0.9)
N, D = x.shape
running_mean = bn_param.get('running_mean', np.zeros(D, dtype=x.dtype))
running_var = bn_param.get('running_var', np.zeros(D, dtype=x.dtype))
out, cache = None, None
if mode == 'train':
#######################################################################
# TODO: Implement the training-time forward pass for batch norm. #
# Use minibatch statistics to compute the mean and variance, use #
# these statistics to normalize the incoming data, and scale and #
# shift the normalized data using gamma and beta. #
# #
# You should store the output in the variable out. Any intermediates #
# that you need for the backward pass should be stored in the cache #
# variable. #
# #
# You should also use your computed sample mean and variance together #
# with the momentum variable to update the running mean and running #
# variance, storing your result in the running_mean and running_var #
# variables. #
# #
# Note that though you should be keeping track of the running #
# variance, you should normalize the data based on the standard #
# deviation (square root of variance) instead! #
# Referencing the original paper (https://arxiv.org/abs/1502.03167) #
# might prove to be helpful. #
#######################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
sample_mean = np.mean(x,axis=0)
sample_var = np.mean((x - sample_mean) ** 2, axis=0)
x_hat = (x - sample_mean) / np.sqrt(sample_var + eps)
out = gamma * x_hat + beta
cache = (x, gamma, sample_mean, sample_var, eps, x_hat)
running_mean = momentum * running_mean + (1 - momentum) * sample_mean
running_var = momentum * running_var + (1 - momentum) * sample_var
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
#######################################################################
# END OF YOUR CODE #
#######################################################################
elif mode == 'test':
#######################################################################
# TODO: Implement the test-time forward pass for batch normalization. #
# Use the running mean and variance to normalize the incoming data, #
# then scale and shift the normalized data using gamma and beta. #
# Store the result in the out variable. #
#######################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
x_hat = (x - running_mean) / np.sqrt(running_var + eps)
out = gamma * x_hat + beta
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
#######################################################################
# END OF YOUR CODE #
#######################################################################
else:
raise ValueError('Invalid forward batchnorm mode "%s"' % mode)
# Store the updated running means back into bn_param
bn_param['running_mean'] = running_mean
bn_param['running_var'] = running_var
return out, cache
2. batch normalization backward
实现思路: 通过计算图反向传播计算梯度,较为繁琐,可参考下一个实现
def batchnorm_backward(dout, cache):
"""
Backward pass for batch normalization.
For this implementation, you should write out a computation graph for
batch normalization on paper and propagate gradients backward through
intermediate nodes.
Inputs:
- dout: Upstream derivatives, of shape (N, D)
- cache: Variable of intermediates from batchnorm_forward.
Returns a tuple of:
- dx: Gradient with respect to inputs x, of shape (N, D)
- dgamma: Gradient with respect to scale parameter gamma, of shape (D,)
- dbeta: Gradient with respect to shift parameter beta, of shape (D,)
"""
dx, dgamma, dbeta = None, None, None
###########################################################################
# TODO: Implement the backward pass for batch normalization. Store the #
# results in the dx, dgamma, and dbeta variables. #
# Referencing the original paper (https://arxiv.org/abs/1502.03167) #
# might prove to be helpful. #
###########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
x, gamma, mean, var, eps, x_hat = cache
m = x.shape[0]
dx_hat = dout * gamma
dvar = np.sum(dx_hat * (x - mean) * (-0.5) * np.power((var + eps), -1.5), axis=0)
dmean = np.sum(dx_hat * (-1) / np.sqrt(var + eps), axis=0) + dvar * np.sum(-2 * (x - mean), axis=0) / m
dx = dx_hat / np.sqrt(var + eps) + dvar * 2 * (x - mean) / m + dmean / m
dx_1 = dout * gamma
dx_2_b = np.sum((x - mean) * dx_1, axis=0)
dx_2_a = ((var + eps) ** -0.5) * dx_1
dx_3_b = -0.5 * ((var + eps) ** -1.5) * dx_2_b
dx_4_b = dx_3_b * 1
dx_5_b = np.ones_like(x) / m * dx_4_b
dx_6_b = 2 * (x - mean) * dx_5_b
dx_7_a = dx_6_b * 1 + dx_2_a * 1
dx_7_b = dx_6_b * 1 + dx_2_a * 1
dx_8_b = -1 * np.sum(dx_7_b, axis=0)
dx_9_b = np.ones_like(x) / m * dx_8_b
dx_10 = dx_9_b + dx_7_a
dx = dx_10
dgamma = np.sum(dout * x_hat, axis=0)
dbeta = np.sum(dout, axis=0)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
###########################################################################
# END OF YOUR CODE #
###########################################################################
return dx, dgamma, dbeta3. batch normalization backward 更为简洁的实现
实现思路:
通过论文[1]所给公式计算,可以自己推导一遍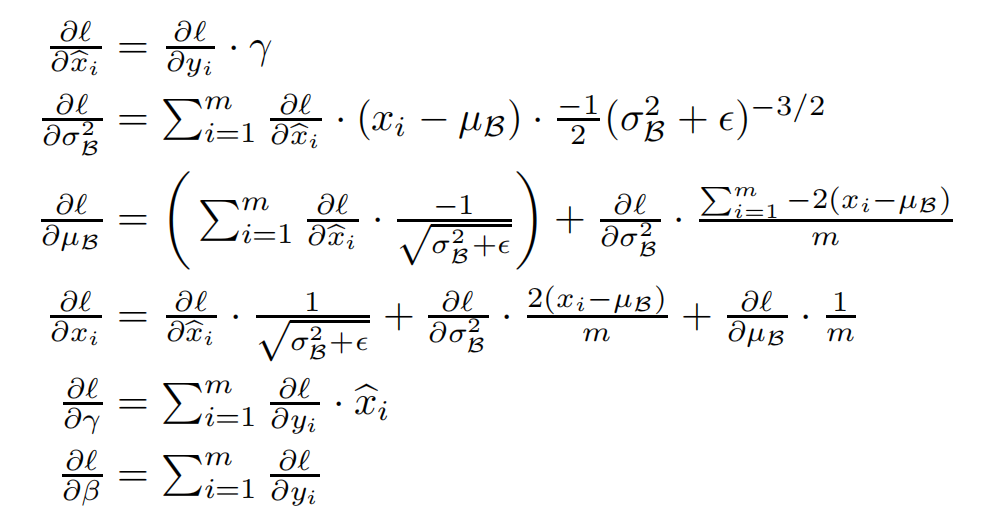
def batchnorm_backward_alt(dout, cache):
"""
Alternative backward pass for batch normalization.
For this implementation you should work out the derivatives for the batch
normalizaton backward pass on paper and simplify as much as possible. You
should be able to derive a simple expression for the backward pass.
See the jupyter notebook for more hints.
Note: This implementation should expect to receive the same cache variable
as batchnorm_backward, but might not use all of the values in the cache.
Inputs / outputs: Same as batchnorm_backward
"""
dx, dgamma, dbeta = None, None, None
###########################################################################
# TODO: Implement the backward pass for batch normalization. Store the #
# results in the dx, dgamma, and dbeta variables. #
# #
# After computing the gradient with respect to the centered inputs, you #
# should be able to compute gradients with respect to the inputs in a #
# single statement; our implementation fits on a single 80-character line.#
###########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
x, gamma, mean, var, eps, x_hat = cache
m = x.shape[0]
dx_hat = dout * gamma
dvar = np.sum(dx_hat * (x - mean) * (-0.5) * np.power((var + eps), -1.5), axis=0)
dmean = np.sum(dx_hat * (-1) / np.sqrt(var + eps), axis=0) + dvar * np.sum(-2 * (x - mean), axis=0) / m
dx = dx_hat / np.sqrt(var + eps) + dvar * 2 * (x - mean) / m + dmean / m
dgamma = np.sum(dout * x_hat, axis=0)
dbeta = np.sum(dout, axis=0)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
###########################################################################
# END OF YOUR CODE #
###########################################################################
return dx, dgamma, dbeta4. layer normalization forward & backward
实现思路: 根据论文[2],layer normalization与batch normalization在实现上极为相似,只需加入转置
def layernorm_forward(x, gamma, beta, ln_param):
"""
Forward pass for layer normalization.
During both training and test-time, the incoming data is normalized per data-point,
before being scaled by gamma and beta parameters identical to that of batch normalization.
Note that in contrast to batch normalization, the behavior during train and test-time for
layer normalization are identical, and we do not need to keep track of running averages
of any sort.
Input:
- x: Data of shape (N, D)
- gamma: Scale parameter of shape (D,)
- beta: Shift paremeter of shape (D,)
- ln_param: Dictionary with the following keys:
- eps: Constant for numeric stability
Returns a tuple of:
- out: of shape (N, D)
- cache: A tuple of values needed in the backward pass
"""
out, cache = None, None
eps = ln_param.get('eps', 1e-5)
###########################################################################
# TODO: Implement the training-time forward pass for layer norm. #
# Normalize the incoming data, and scale and shift the normalized data #
# using gamma and beta. #
# HINT: this can be done by slightly modifying your training-time #
# implementation of batch normalization, and inserting a line or two of #
# well-placed code. In particular, can you think of any matrix #
# transformations you could perform, that would enable you to copy over #
# the batch norm code and leave it almost unchanged? #
###########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
x = x.T
sample_mean = np.mean(x, axis=0)
sample_var = np.mean((x - sample_mean) ** 2, axis=0)
x_hat = (x - sample_mean) / np.sqrt(sample_var + eps)
out = gamma * x_hat.T + beta
cache = (x, gamma, sample_mean, sample_var, eps, x_hat)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
###########################################################################
# END OF YOUR CODE #
###########################################################################
return out, cache
def layernorm_backward(dout, cache):
"""
Backward pass for layer normalization.
For this implementation, you can heavily rely on the work you've done already
for batch normalization.
Inputs:
- dout: Upstream derivatives, of shape (N, D)
- cache: Variable of intermediates from layernorm_forward.
Returns a tuple of:
- dx: Gradient with respect to inputs x, of shape (N, D)
- dgamma: Gradient with respect to scale parameter gamma, of shape (D,)
- dbeta: Gradient with respect to shift parameter beta, of shape (D,)
"""
dx, dgamma, dbeta = None, None, None
###########################################################################
# TODO: Implement the backward pass for layer norm. #
# #
# HINT: this can be done by slightly modifying your training-time #
# implementation of batch normalization. The hints to the forward pass #
# still apply! #
###########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
x, gamma, mean, var, eps, x_hat = cache
m = x.shape[0]
dx_hat = (dout * gamma).T
dvar = np.sum(dx_hat * (x - mean) * (-0.5) * np.power((var + eps), -1.5), axis=0)
dmean = np.sum(dx_hat * (-1) / np.sqrt(var + eps), axis=0) + dvar * np.sum(-2 * (x - mean), axis=0) / m
dx = dx_hat / np.sqrt(var + eps) + dvar * 2 * (x - mean) / m + dmean / m
dx = dx.T
dgamma = np.sum(dout * x_hat.T, axis=0)
dbeta = np.sum(dout, axis=0)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
###########################################################################
# END OF YOUR CODE #
###########################################################################
return dx, dgamma, dbetaSummary
本次作业主要是batch normalization 和 layer normalization 层的前向、反向传播实现,通过BN、LN层可大大加快神经网络训练
速度,并且加入BN层对于权重的初始化较不敏感。作业难点在与梯度计算,但论文已给出相关公式。
Reference
- [1] Sergey Ioffe and Christian Szegedy, “Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift”, ICML 2015.
- [2] Ba, Jimmy Lei, Jamie Ryan Kiros, and Geoffrey E. Hinton. “Layer Normalization.” stat 1050 (2016): 21.
- CS231n课程笔记翻译:神经网络笔记 2
- Batch-Normalization(批量归一化)
- cs 231 Batch Normalization 求导推导及代码复现(BN,LN
- lightaime/cs231n



